1 - Single population models

A first population model

Our aim in this course is to model the dynamics of populations over time. By ‘population’ we simply mean some collection of individuals that are subject to the same underlying mechanisms. For example, we may consider the human population of Sheffield, or the tapir population of South America, or the maize crop population of a field in Nigeria. In later chapters we will move to smaller biological scales, considering perhaps less intuitive definitions of populations, such as of cells in the body, or proteins within cells. However, a key message to take from this course is that we can consider any and all biological populations in the same way from a modelling perspective, and subject to the same fundamental of biological mechanisms.

We will model these dynamics using oridnary differential equations, and our focus will be purely on how the size of a population varies over time. We will not consider where individuals are in space - this would likely require extending our methods to partial differential equation models, and plenty of excellent courses and textbooks can be found to explore such systems. When we talk about the ‘size’ of a population, we might think we mean the number of individuals in the population. However, as we will be using ordinary differential equations we need our variables to be continuous, not discrete. We will therefore instead keep track of a population’s density - the number of individuals within some unit area.

Introducing our mathematical notation, we might call \(N(t)\) the density of individuals within our population at time \(t\). We now wish to write down an ordinary differential equation that describes its dynamics - that is what causes the population to increase or decrease. Our first modelling challenge, then, is to decide what mechanisms we should include. Using some biological intuition for the simplest possible population we can think of, we might expect our model to look something like,

(1)\[\begin{align} \frac{dN}{dt} &= \textrm{births} -\textrm{deaths}. \end{align}\]

Now to make any mathematical progress we will need to decide on functional forms for each of these mechanisms. This is another important modelling decision, and will depend on the specific biology. There are three main forms we might use:

• constant rate, \(\textrm{births}=B\). This would be suitable when new individuals appear in the environment at some constant rate, for example due to migration, or production of cells by the body.

• per-capita rate, \(\textrm{births}=bN\). This would be suitable when each individual produces offspring at a certain rate, such that there are more offspring produced when the population is larger.

• density-dependent rate, \(\textrm{births}=b(N)N\). This would be suitable if the per-capita rate is not fixed but instead varies with the population size, for example if high density means more competition for resources and thus lower growth. The form of this function will again depend on the biology, though there are common functions we tend to use.

For our basic model, per-capita rates for birth and death seem the most obvious choice. Our model is thus,

(2)\[\begin{align} \frac{dN}{dt}&= bN - dN \\ &= rN, \end{align}\]

where the parameter \(r=b-d\) is the growth rate of our population. We therefore have a first-order, linear ordinary differential equation. Such ODEs are readily solved using either separation of variables or integrating factors. Once ready, have a go at the exercise.

Have a go

Either by separation of variables or integrating factors show that,

(3)\[\begin{equation} N(t) = N(0)e^{rt}, \end{equation}\]

Click for solution

First we gather all the terms with \(N\) to the left-hand side and everything else on the right-hand side, giving,

(4)\[\begin{equation} \frac{dN}{N} = rdt. \end{equation}\]

Then we integrate both sides, giving,

(5)\[\begin{equation} \ln(N) = rt+C, \end{equation}\]

where \(C\) is a constant of integration. If we then take the exponential of both sides we get,

(6)\[\begin{equation} N(t) = e^{rt+C}=C_1e^{rt}, \end{equation}\]

where \(C_1=e^{C}\). To replace this constant we use the initial condition that at time \(t=0\) we have a density of \(N(0)\). Substituting these values in we find that \(C_1=N(0)\), leaving us with the final solution,

(7)\[\begin{equation} N(t) = N(0)e^{rt}, \end{equation}\]

as required.

This predicts exponential growth of the population for \(r>0\) and exponential decline for \(r<0\).

Limits to population growth: The logistic equation

In that last exercise we found that if \(r>0\) - meaning births are greater than deaths - our population will continue growing to infinitely large densities. This is, we can hopefully agree, a tad unrealistic. We should not lose heart at this point, though. A model that produces unrealistic results is still helpful to us, because it will point the way towards how we can develop an improved version.

What might we have failed to take into account in our model? One answer is that as the population grows the environment will become limiting in some way. For example, individuals need space and nutrients to live and reproduce. These resources will be consumed by the population more and more as the population grows, likely leading to reduced birth and/or death rates. So while our assumptions may hold at low population densities, they will break down at higher densities. Our simple model has shown us that we need to take this into consideration if we are to understand the population dynamics.

Given this, choosing a density-dependent growth rate starts to look like a better assumption. A relatively simple and intuitive way to set a limit on population growth is to assume that there is a fixed carrying capacity for the population, for example due to the available space or nutrients. We assume that as the population approaches this carrying capacity, the overall growth rate approaches zero, and once the population goes above this value the growth rate becomes negative. The simplest implementation of this is to assume that \(r\) decreases linearly with \(N\):

\[ r(N) = r_0\left(1 - \frac{N}{K}\right), \]

where \(r_0\) (the basic reproductive rate) and \(K\) (the carrying capacity) are positive constants. Our ordinary differential equation for the dynamics of our population is then

(8)\[\begin{equation} \frac{dN}{dt}=r_0N\left(1 - \frac{N}{K}\right). \end{equation}\]

This equation is known as the logistic growth equation and is an example of intra-specific competition.

A useful step: non-dimensionalisation

We can continue our analysis with the model in this form using methods for solving single ordinary differential equations. However, before continuing with our analysis we shall introduce the useful technique of non-dimensionalising our model. This is often - though not always - done to models to simplify some of the later working. It can both reduce the number of parameters in the model and give us insight in to the scales at which biological processes operate.

Non-dimensionalisation involves combining variables and/or parameters from the model in biologically and mathematically helpful ways. For example, a natural scale for the population level is \(K\), so we can define the non-dimensional population variable \(n=N/K\) (\(n\) is non-dimensional becaus eboth \(N\) and \(K\) have units 1/[density], so \(n\) is a dimensionless number). The equation then becomes

\[ \frac{dn}{dt}=\frac{d(N/K)}{dt}=\frac{1}{K}\frac{dN}{dt}=r_0n(1 - n). \]

We can also note that a natural time scale for the dynamics is \(1/r_0\), such that we can take a new non-dimensional time variable, \(\tau = r_0t\), and the final non-dimensional model equation is

(9)\[\begin{equation} \frac{dn}{d\tau}=\frac{dn}{d(r_0t)}=\frac{1}{r_0}\frac{dn}{dt}=n(1 - n).\label{logeq} \end{equation}\]

As you can see, by using two simple substitutions we have arrived at a very simple equation.

Model analysis

Even though this equation is non-linear (we have an \(n^2\) term), we can still find an explicit solution for it. By separation of variables, we can write this as,

(10)\[\begin{equation} \int\frac{dn}{n(1-n)} = \int r_0 d\tau, \end{equation}\]

If we use partial fractions to rewrite the fraction on the left-hand side as the sum of two terms, we reach an initial solution of,

(11)\[\begin{align} &\ln(n)-\ln(1-n) = r_0\tau+C,\\ \implies &\frac{n}{1-n}=e^Ce^{r_0\tau}, \end{align}\]

where \(C\) is a constant of integration and \(\ln\) denotes the natural logarithm. Letting the initial condition be \(n(0)=n_0\) and rearranging, we arrive at the final solution,

(12)\[\begin{equation} n(\tau) = \frac{n_0}{n_0+(1-n_0)e^{-\tau}}. \end{equation}\]

(Alternatively a suitable substitution can be chosen to evaluate the integrals. It is often true in mathematical mdoelling that there are multiple ways to arrive at a solution, and embracing this diversity of approach can be very useful).

Examples of the dimensional solution for different values of \(r_0\) are shown in the figure.

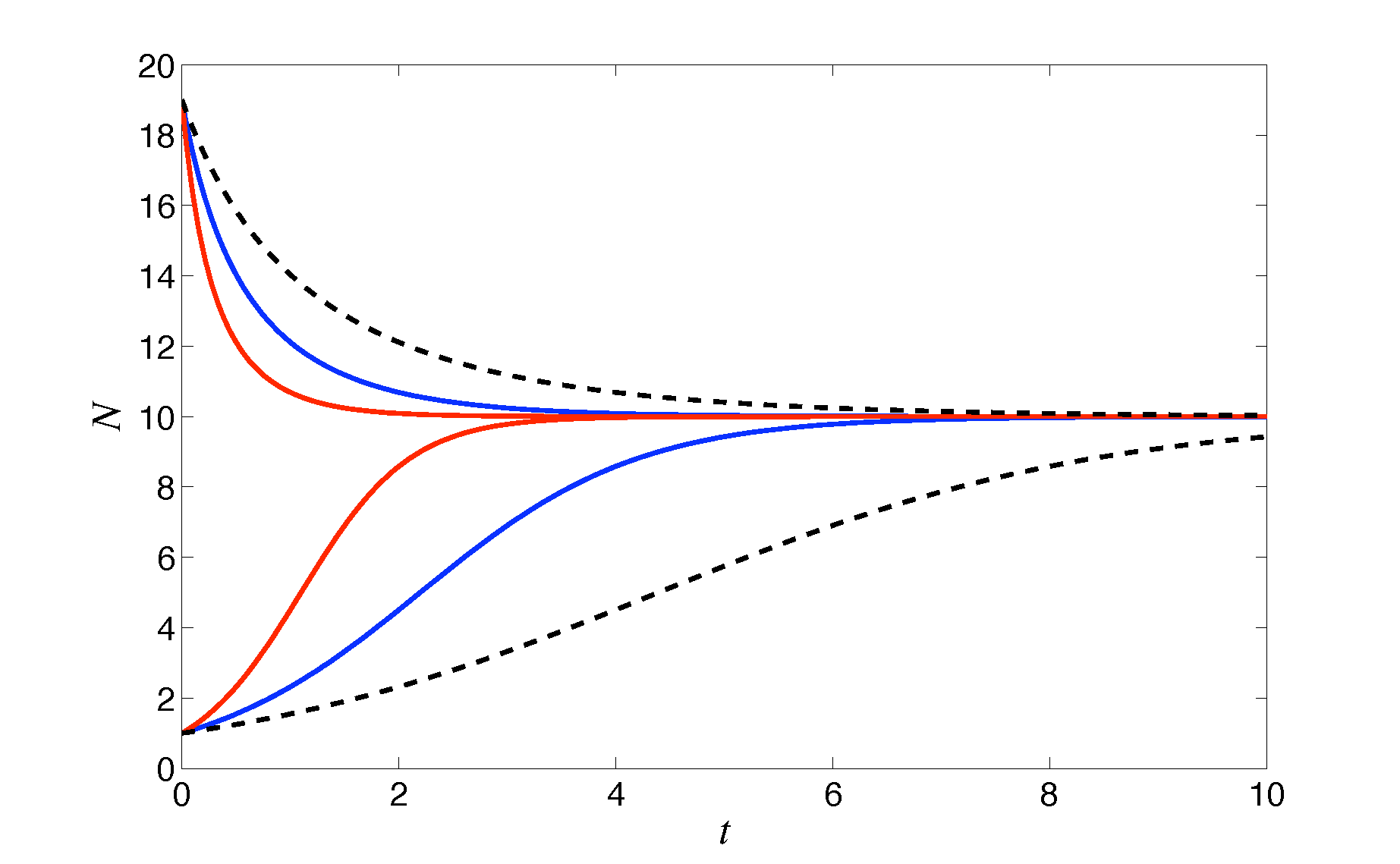
Figure: example time-courses of the logistic model, with \(K=10\) and different values of \(r_0\) and initial conditions.

However, we can in fact gain a good deal of qualitative information about this model directly from the equation without having to spend the few minutes invovled in deriving that explicit solution. Specifically, we can see:

• for \(0<n<1\), \(dn/d\tau>0\)

• for \(n>1\), \(dn/d\tau<0\)

(note that it makes no biological sense to worry about \(n<0\)). There are two values of \(n\) for which \(dn/d\tau=0\), at \(n=0\) and \(n=1\), which are the equilibria of the system. Therefore for any starting value of \(n>0\) the population should move towards a final state of \(n=1\), suggesting that the equilibrium at \(n=0\) is unstable and the equilibrium at \(n=1\) is stable. We can think about this more by sketching the curve \(dn/d\tau\) vs \(n\).

Have a go

Sketch the curve \(dn/d\tau\) vs \(n\) and use it to identify the key aspects of the system.

Click for solution

On this sketch we can mark our equilibria at \(n=0\) and \(n=1\) and then consider the wider behaviour by considering the curve \(dn/d\tau\). For convenience let us call \(dn/d\tau=f(n)\), and then look at what happens nearby the equilibria by linearisation.

• At \(n=0\), the gradient of the curve \(df/dn\) is positive, meaning \(dn/d\tau<0\) for \(n<0\) (we don’t really mind about the actual values here since \(n<0\) is biologically meaningless, but it is still useful mathematically) and \(dn/d\tau>0\) for \(n>0\). As such if we start with a population density a small distance away from \(n=0\) we will always end up moving further away from it - it is unstable.

• At \(n=1\), we have \(df/dn\) negative, meaning \(dn/d\tau>0\) for \(n<1\) and \(dn/d\tau<0\) for \(n>1\), As such if we start with a population density a small distance away from \(n=1\) we will always move in towards this equilibrium - it is stable.

We can also mark on the qualitative direction of trajectories on the x-axis, giving a phase line. Notice, then, that we have fully described the possible behaviours of this system without having to explicitly solve the equation.

Case study: spruce budworm

Spruce budworm is an insect that lives in spruce and fir forests in the USA and Canada. (This example is borrowed from the classic Mathematical Biology textbook by J. D. Murray, with a few tweaks). While they mostly exist at low numbers, there are periodic explosions of budworm populations that devestate the forests. Let us assume that on their own, the budworm populaitons follow the logistic growth model we have just studied. An additional feature of budworm dynamics is that they are predated by birds. We might then describe the dynamcis of budworm by the following equation,

(13)\[\begin{equation} \frac{dN}{dt}=r_0N\left(1 - \frac{N}{K}\right)-P(N), \end{equation}\]

where \(P(N)\) describes the rate of predation (note that we do not explicitly consider the bird population dynamics). What should \(P(N)\) look like? Should it be constant, a fixed per-capita rate, or some other density-dependent fucntion? First, we might reasonably assume that as more food becomes available, the more the birds will eat, so predation should increase with budworm density. However, we should also note that birds cannot eat an infinite amount, and that the rate of predation should therefore saturate at high budworm densities. We therefore need a density-dependent function. We might then give an explicit model as,

(14)\[\begin{equation} \frac{dN}{dt}=r_0N\left(1 - \frac{N}{K}\right)-\frac{\rho N}{N+A} \end{equation}\]

This form for the predation function is a very commonly used one in mathematical biology models. What are the possible outcomes of this model? We might start by finding equilibria as before, but we will quickly find ourselves bogged down. Instead, let’s take a qualitative approach and use curve-sketching to explore the possible outcomes. The above model can be written as,

(15)\[\begin{equation} \frac{dN}{dt}=N\left[r(N)-p(N)\right], \end{equation}\]

where \(r(N)=r_0(1-N/K)\) and \(p(N)=\rho/(N+A)\). We know that an equilibrium occurs where \(r(N)-p(N)=0\), which will be when the two curves cross. Below we sketch these two curves, \(r(N)\) and \(p(N)\), in the three possible combinations,

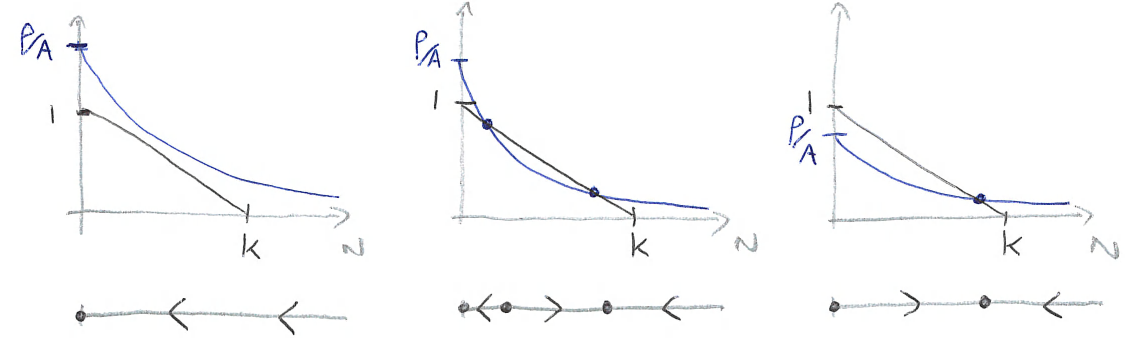
Figure: Sketches of \(r(N)\) and \(p(N)\) to assess stability of spruce budworm model for three different cases.

What happens in each case?

1. Predation by the birds is very high and the two curves never cross, and \(dN/dt<0\) for all \(N>0\). Therefore the insect population is always reducing until it reaches extinction, with \(N=0\) a stable equilibrium.

2. Predation has weakened somewhat and two new equilibria appear, one stable and one unstable. We now have bistability - where two different equilibria are stable, but which one we go to depends on the initial conditions.

3. Predation is very weak and we now only have one equilibrium for \(N>0\), at high budworm densities. We also see now that \(N=0\) is no longer stable, and the budworm population will always reach this high equilibrium density.

What do these results tell us? That pest outbreaks such as the spruce budworm are likely to be driven by the pressure from predation. We can also see that, due to the bistability, sudden outbreaks can occur if there are relatively small changes to the environment. We have achieved this insight without having to do any detailed mathematical derivations, but by applying mathematical reasoning and biological interpretation - these are two key skills we will develop over this course.

Have a go: coding

To use the code, click the rocket icon at the top of the page, and then click Colab. This will take you to a live version of this page where you can run the code.

Scroll down to the code cell below and either click in the cell and hit Shift-Enter, or click on the ‘Play’ icon in the top-left of the cell. You may see a warning about loading content from Github - click ‘Run anyway’.

This code will produce a time-course and plot of rates for the dynamics of spruce budworm subject to predation by birds. The dynamics are governed by the following ordinary differential equation: \(dN/dt=r0N(1−N/K)−ρN/(N+A)\) .

After it has run, below the code cell you will see a set of sliders to choose the values of the 4 parameters (though I suggest you focus on varying \(\rho\)). You will see the two plots appear - a time course of the dynamics, and the plots of the growth and predation rates. The plots will automatically update as you change the values.

Note that the sliders/plot in this webpage are static and do not change - you need to load the Colab version for them to work.

Show code cell source Hide code cell source

################
# HAVE A GO: CODING
###############

# Import the necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
import ipywidgets as widgets
from ipywidgets import interactive


# Create widgets
rhow=widgets.FloatSlider(min=0, max=20, step=1, value=20, description='\rrho')
r0w=widgets.FloatSlider(min=0, max=10, step=1, value=5, description='r_0')
Kw=widgets.FloatSlider(min=0, max=15, step=1, value=10, description='K')
Aw=widgets.FloatSlider(min=0, max=2.5, step=0.5, value=1, description='A')


# Function for the population dynamics
def budworm(N,t,r0,K,rho,A):
    dN = r0*N*(1-N/K)-rho*N/(N+A)
    return dN

# Function called by the widget
def runbudworm(rho=20,r0=5,K=10,A=1):
    
    # Find parameter values and ICs from widgets
    N0=8
    N1=2

    # Timespan
    tc = np.linspace(0, 10, 1000)  
    
    # Run the ODEs with the 2 different ICs
    Nc = odeint(budworm, N0, tc,args=(r0,K,rho,A))
    Nd = odeint(budworm, N1, tc,args=(r0,K,rho,A))
    
    # Nullclines
    nn=np.linspace(0,15,100)
    rnull=r0*(1-nn/K)
    pnull=rho/(nn+A)
    
    # Plotting commands
    plt.rcParams['figure.figsize'] = [12, 4]
    plt.rcParams.update({'font.size': 16})
    fig, (ax1, ax2) = plt.subplots(1, 2)
    ax1.plot(tc, Nc[:], "r") 
    ax1.plot(tc, Nd[:], "r:")
    ax1.set(xlabel='Time', ylabel='Densities')
    ax1.axis([0,10,0,10])
    ax2.plot(nn,rnull,'r',label='r(N)')
    ax2.plot(nn,pnull,'k',label='p(N)')
    ax2.set(xlabel='$N$', ylabel='Rates')
    ax2.legend()
    ax2.axis([0, 12, 0, 10])
    plt.show()
    
    return()

# Display the widgets
#w = interactive(runbudworm,rho=(0,20,1),r0=(0,10,1),K=(5,15,1),A=(0,2.5,0.5))
#display(w)

ui1 = widgets.HBox([rhow])
ui2 = widgets.HBox([r0w, Kw, Aw])
out = widgets.interactive_output(runbudworm, {'rho': rhow, 'r0': r0w, 'K': Kw, 'A': Aw})
   
display(ui1,ui2,out)

3 key points

1. Parameters in a model represent rates of change, and their functional form implies how that process works.

2. The logistic equation goes to a long-term equilibrium, and we do not need to explicitly solve it to understand its key behaviours.

3. Sudden outbreaks of spruce budworm can occur if there is a small change in the level of predation.