Lecture 18. Modelling projectile motion

Last lecture we focused predominantly on models of motion in one dimension with constant acceleration, with a particular emphasis on acceleration due to gravity. This is fine for modelling things that move vertically up and down, but often movement occurs in a horizontal direction, too. Here we will examine motion under the effect of constant acceleration where there are components of motion both parallel and perpendicular to the direction of the acceleration.

A paradigmatic example of this is the motion of projectiles close to the Earth’s surface. When an object is propelled in a non-vertical direction, its motion will be governed by the acceleration due to gravity. However, the object will also have some horizontal movement.

If we are modelling a projectile that has a non-vertical initial velocity, we can write the initial velocity as

\[ \begin{equation*} \mathbf{u}=x_{0} \mathbf{i}+y_{0} \mathbf{j}+z_{0} \mathbf{k} \tag{222} \end{equation*} \]

where \(x_{0}, y_{0}\), and \(z_{0}\) are constants. Since we can choose our horizontal co-ordinates however we want, it is convenient to assume the horizontal component of movement is all in the \(\mathbf{i}\) direction. In other words, without loss of generality we set \(y_{0}=0\) so that

\[ \begin{equation*} \mathbf{u}=x_{0} \mathbf{i}+z_{0} \mathbf{k} \tag{223} \end{equation*} \]

Suppose that the projectile is released at an angle of \(\theta\) to the horizontal. Then \(x_{0}=V \cos (\theta)\) and \(z_{0}=V \sin (\theta)\) where \(V\) is the initial speed of the projectile (Figure 27).

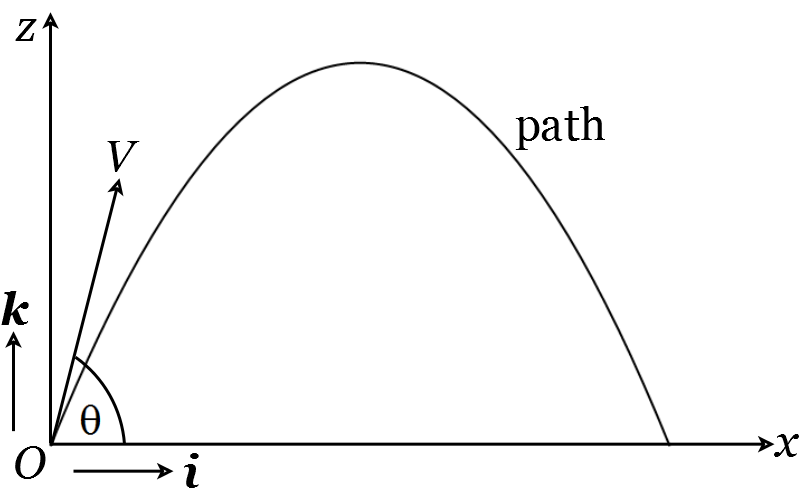
Figure 27: A projectile released at an angle \(\theta\) from the horizontal.

Now, since the acceleration due to gravity is in the negative \(\mathbf{k}\)-direction, we have \(\mathbf{a}=-g \mathbf{k}\), where \(g\) is the gravitational constant. We can now put these expressions for \(\mathbf{u}\) and \(\mathbf{a}\) into Equation (211) (which says \(\mathbf{v}(t)=\mathbf{a} t+\mathbf{u}\) ). This gives

\[ \begin{equation*} \mathbf{v}(t)=-g \mathbf{k} t+V \cos (\theta) \mathbf{i}+V \sin (\theta) \mathbf{k} \tag{224} \end{equation*} \]

Writing \(\mathbf{v}(t)=\dot{x}(t) \mathbf{i}+\dot{z}(t) \mathbf{k}\), we have

\[\begin{split} \begin{align*} & \dot{x}(t)=V \cos (\theta) \tag{225}\\ & \dot{z}(t)=V \sin (\theta)-g t \tag{226} \end{align*} \end{split}\]

which are, respectively, the horizontal and vertical components of the velocity. Similarly, we can use Equation (213) to find the horizontal and vertical components of the projectile’s location, \(x(t)\) and \(z(t)\) respectively, as follows

\[\begin{split} \begin{align*} \mathbf{r}(t) & =\frac{1}{2} \mathbf{a} t^{2}+\mathbf{u} t \\ & =-\frac{g}{2} \mathbf{k} t^{2}+V \cos (\theta) \mathbf{i} t+V \sin (\theta) \mathbf{k} t \\ & =x(t) \mathbf{i}+z(t) \mathbf{k} \tag{227} \end{align*} \end{split}\]

which gives

\[\begin{split} \begin{align*} & x(t)=V t \cos (\theta) \tag{228}\\ & z(t)=V t \sin (\theta)-\frac{1}{2} g t^{2} \tag{229} \end{align*} \end{split}\]

18.1 The shape of a projectile’s path

The path of a parabola turns out to form a well-known shape. We demonstrate this by rearranging Equations (228-229) to give an expression for \(z\) in terms of \(x\). For this, it is convenient to drop the explicit dependence of \(x\) and \(z\) on \(t\), to write

\[\begin{split} \begin{align*} & x=V t \cos (\theta) \tag{230}\\ & z=V t \sin (\theta)-\frac{1}{2} g t^{2} \tag{231} \end{align*} \end{split}\]

Equation (230) rearranges to give

\[ \begin{equation*} t=\frac{x}{V \cos (\theta)} \tag{232} \end{equation*} \]

which we can put into Equation (231) to give

\[\begin{split} \begin{align*} z & =\frac{V x \sin (\theta)}{V \cos (\theta)}-\frac{g x^{2}}{2 V^{2} \cos ^{2}(\theta)} \\ & =x \tan (\theta)-x^{2} \frac{g \sec ^{2}(\theta)}{2 V^{2}} \\ & =a x-b x^{2} \tag{233} \end{align*} \end{split}\]

where \(a=\tan (\theta)\) and \(b=g \sec ^{2}(\theta) /\left(2 V^{2}\right)\) are constants. This is a quadratic function, so the shape of the projectile’s path is a parabola.

Example 28

A player for Sheffield Bruins baseball club hits a ball at a height of 1 meter above the ground. The ball’s initial speed is \(90mph\) (~\(40m/s\)) at an angle of \(\frac{\pi}{6}\) radians above the horizontal. Find the horizontal distance from the person to the place where the ball first bounces, assuming \(g=9.8\).

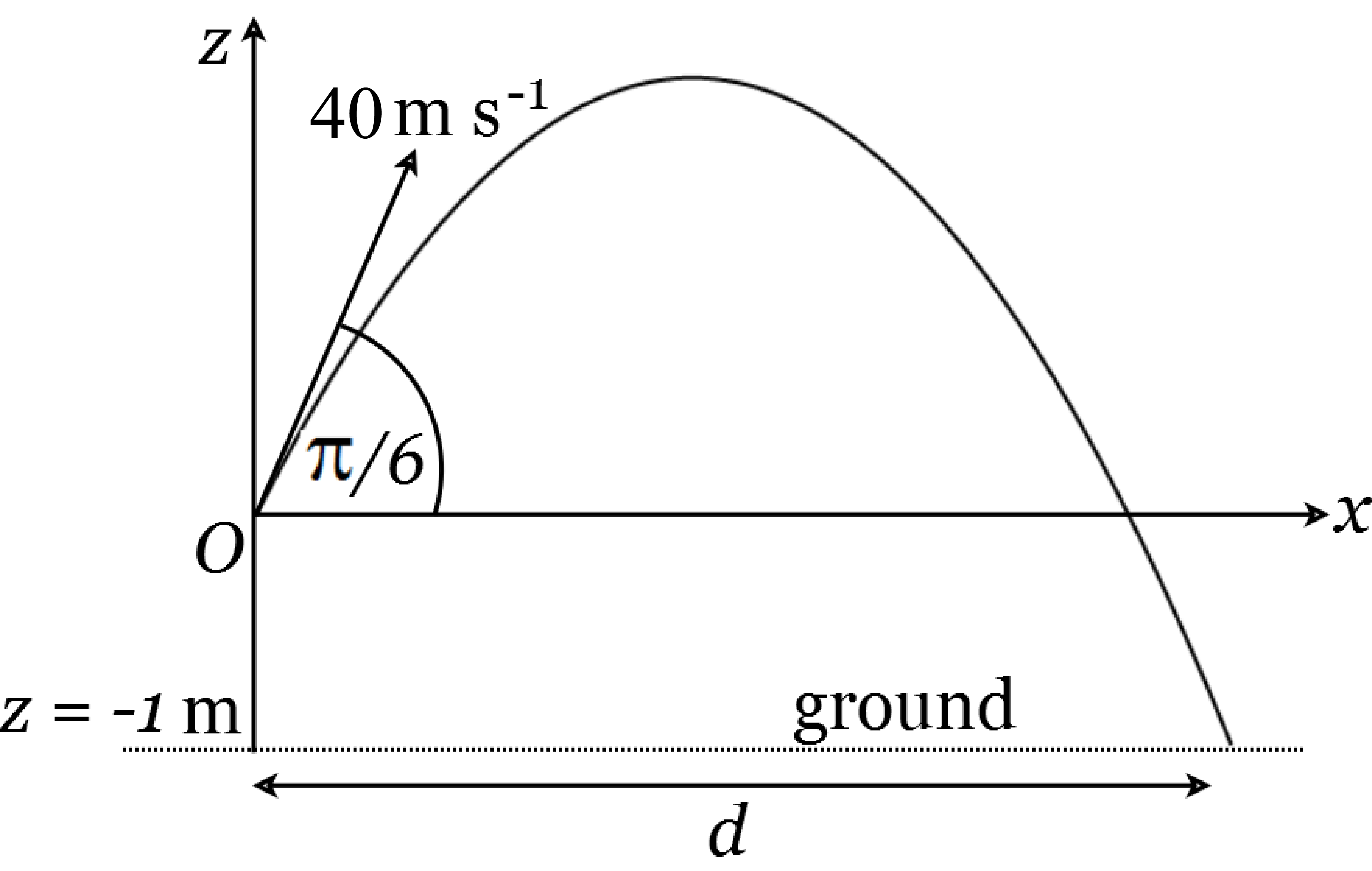
Figure 28: The trajectory of a ball.

Solution.

As usual, we start with a sketch (Figure 28) Let the vertical height of the ball be \(z \mathrm{~m}\) above the point of projection and let the ball be \(x \mathrm{~m}\) horizontally from the person. Then

\[ \begin{equation*} z=x \tan (\theta)-\frac{g x^{2}}{2 V^{2}} \sec ^{2}(\theta) \tag{234} \end{equation*} \]

where \(V=40, g=9.8\) and \(\theta=\frac{\pi}{6}\). Then we have, working to three significant figures,

\[ \begin{equation*} z=0.577 x-0.00408 x^{2} \tag{235} \end{equation*} \]

The ball reaches the ground when \(z=-1, x=d\). This gives

\[\begin{split} \begin{align*} & -1=0.577 d-0.00408 d^{2} \\ \Longrightarrow & 0.00408 d^{2}-0.577 d-1=0 \\ \Longrightarrow & d=\frac{0.577 \pm \sqrt{0.577^{2}+4 \times 0.00408}}{2 \times 0.00408} \tag{236} \end{align*} \end{split}\]

Since \(d\) must be positive, we have \(d \approx 143\), so the ball first bounces 143m (470 feet) away. (At the Bruins home ground this would probably mean a home run and a broken car window).

Lecture 18 Homework exercises

Exercise 39.

A ball is thrown with an initial speed of \(30 \mathrm{~ms}^{-1}\) to strike a target at a horizontal distance of 40 m and at a height of 10 m above the ground. Taking \(g=9.8 \mathrm{~ms}^{-2}\), determine the possible angles of projection above the horizontal.

Exercise 40.

A stone is thrown with initial speed \(30 \mathrm{~ms}^{-1}\) at an angle \(\alpha\) to the horizontal, where \(\tan \alpha=\frac{4}{3}\). The stone hits the ground after \(T\) seconds at a horizontal distance of 90 m from the point of projection and \(k \mathrm{~m}\) below it. Using \(g=9.8 \mathrm{~ms}^{-2}\), find the values of \(T\) and \(k\). Find the velocity of the stone when it strikes the ground.